こんにちは
偏差値が100を越えることは何となく知っているけど、どのような条件なのか改めて調べたら、偏差値について理解が深まりました。
- 偏差値の求め方と、偏差値100以上をとる条件
目次
Wikipediaでは、偏差値は、
偏差値(へんさち、英: standard score)とは、データの値が、平均50、標準偏差10のデータに変換(正規化)したときに示す値のことである。
https://ja.wikipedia.org/wiki/%E5%81%8F%E5%B7%AE%E5%80%A4
と説明されています。
偏差値は、データの値が正規分布に従っていることを前提として計算されます。
データの平均値を偏差値50となるように変換した値とありますが、どのように変換するのかなど、これだけではよく分からないので偏差値の求め方を勉強しました。
偏差値を求めるには、
平均値 → 偏差 → 分散 → 標準偏差 → 偏差値
の順に計算していきます。
平均値\(\;\bar{ x }\;\)は、
$$ \begin{align} \bar{x} &= \frac{1}{n}(x_1 + x_2 + \cdots + x_n) \\ &= \frac{1}{n}\sum_{i=1}^{n} x_i \end{align} $$と求めることができます。\(n\;\)はデータの総数を表します。
偏差とは、個々のデータと平均値の差のことです。
$$ 偏差= x_i – \bar{x} $$\(n\;\)個のデータそれぞれの偏差を求めます。
分散\(\;s^2\;\)とは、データ分布の散らばり具合のことです。
偏差を二乗して平均をとります。
$$ \begin{align} s^2 &= \frac{1}{n}[(x_1 – \bar{x})^2 + (x_2 – \bar{x})^2 + \cdots + (x_n – \bar{x})^2] \\ &=\frac{1}{n}\sum_{i=1}^{n} (x_i – \bar{x})^2 \end{align} $$と計算できます。
標準偏差\(\;s\;\)は、分散の正の平方根と定義されています。
$$ s = \sqrt{\frac{1}{n}\sum_{i=1}^{n} (x_i – \bar{x})^2} $$データの値\(\;x_i\;\)に対する偏差値\(\;T_i\;\)は
$$ T_i = \frac{x_i – \bar{x}}{s} \times 10 + 50 $$と定義されます。(\(\;s\;\)は標準偏差)
文字ばかりでイメージがわかないので、具体的な数字を使って計算します。
テストの点数を想定するのが分かりやすいと思います。
excelを使ってRANDBETWEEN関数で適当な数字を入れて、平均値から分散までを計算してみます。
| A | B | C | D | E | F | 平均 | |
|---|---|---|---|---|---|---|---|
| 得点 | 54 | 69 | 71 | 59 | 55 | 76 | 64 |
| 偏差 | -10 | 5 | 7 | -5 | -9 | 12 | 0 |
| 偏差の2乗 | 100 | 25 | 49 | 25 | 81 | 144 | 70.7 |
分散\(\;s^2\;\)は、偏差の2乗を平均した
$$ s^2 = 70.7 $$となり、標準偏差\(\;s\;\)は、分散の正の平方根をとって
$$ \begin{align} s &= \sqrt{70.7} \\[8pt] &= 8.41 \end{align} $$と計算できました。
なお、excel関数で標準偏差は直接計算することができます(STDEV.P関数(母集団)、STDEV.S関数(標本))。
この標準偏差の値を用いて、各得点の偏差値を出します。
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| 偏差値 | 38.1 | 55.9 | 58.3 | 44.1 | 39.3 | 64.3 |
ところで、偏差値100以上をとる条件はどのようになるのかを考えていました。
偏差値\(\;T_i\;\)は
$$ T_i = \frac{x_i – \bar{x}}{s} \times 10 + 50 $$と表されるので、条件は
$$ \frac{x_i – \bar{x}}{s} \times 10 + 50 \geq 100 $$となるでしょう。これより、
$$ \begin{align} \frac{x_i – \bar{x}}{s} &\geq 5 \\[8pt] x_i &\geq \bar{x} + 5s \end{align} $$となります。
偏差値100以上をとるには、平均値から標準偏差の5倍以上大きい得点を取ればよいと分かりました。
独立行政法人大学入試センターに、大学入試共通テストの結果が掲載されています。
偏差値100となるには、平均点が低く、かつ標準偏差も小さいテストで高得点を取ればよいですが、標準偏差を見ると大体15~20程度に収まっているので、満点でも偏差値70台というところでしょうか。
難易度が調整されているので、偏差値100といった外れ値は出ないようになっています。
「東大模試 偏差値」で検索すると模試の結果を載せている人がたくさんいます。
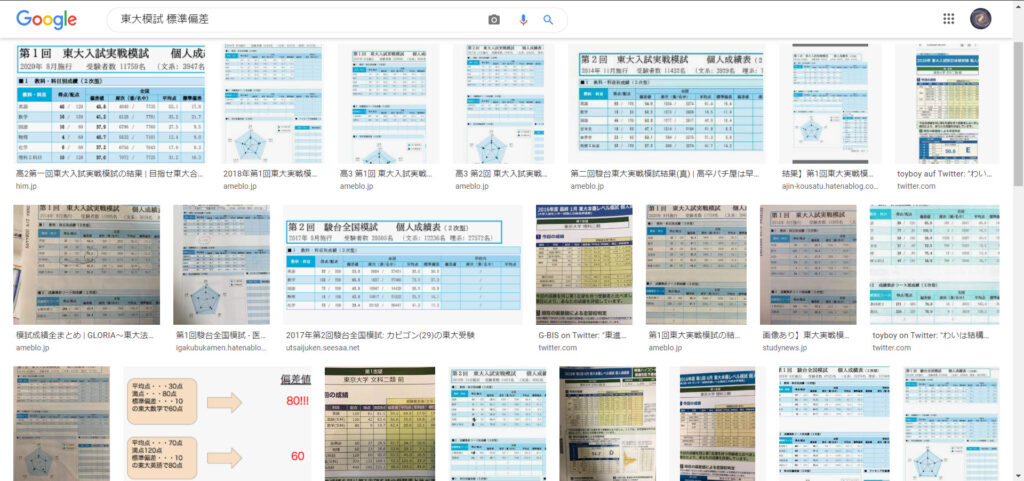
偏差値100以上をとっている人は見つけられませんでしたが、数値を見てみると平均点と標準偏差が十分低い科目もあるので、その科目で高得点を取りさえすれば偏差値100以上は可能であることが分かりました。




自分の高校内であれば、たしか単科(数学)で偏差値が102ぐらいになったことはあります。専用シートに印刷されていたので、何かの模試の結果だったと思います。
当時は、偏差値が100を越えることもあるんだなと思いました。
東大には2~3名合格する程度の高校でした。たぶん平均値のダブルスコアぐらいとる必要がありますね。
コメントありがとうございます。
私も高校の時に、何かの模試で偏差値100を見たことがあります。
やはり100を超えるには平均点が低いことが前提で、かなり突出した点数をとらないといけないですね。